题目

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();     --> 返回 -3.
minStack.pop();
minStack.top();     --> 返回 0.
minStack.min();     --> 返回 -2.

题解

本题的关键在于实现O(1)的min函数。如果min函数每次都遍历整个栈，时间复杂度为O(n)，不符合要求

思路

根据栈先入后出的特性，min值出栈之前，栈的最小值都不会变化

入栈：5 10 9，min=5
5出栈之前，栈的min值一直都是5

当min值更新时，需要记录上一个min值；以防止min值出栈后，无法获取新的min值

入栈：5 10 9，min=[5]
入栈：3 7 6，min=[3,5]
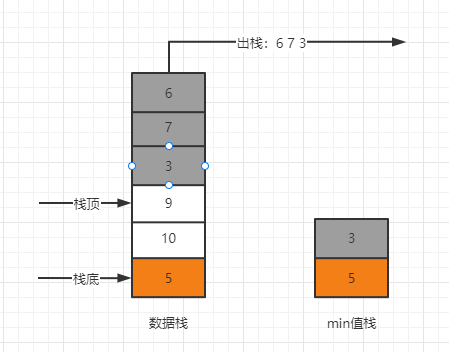
3出栈之前，栈的min值是3
3出栈之后，5出栈之前，栈的min值是5

所以，可以通过辅助栈记录每个阶段的min值，从而实现O(1)的min函数
 

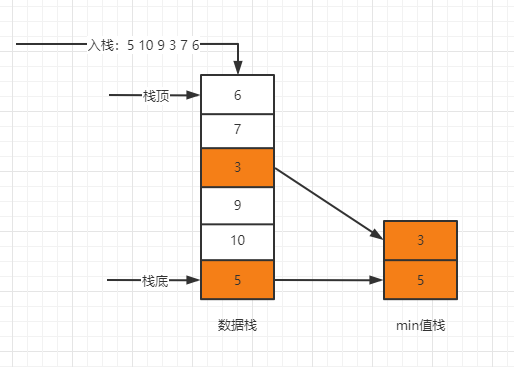
成员变量：

• 维护两个栈，分别用来进行存储数据（dataStack）和最小值（minStack）

初始化：

• 初始化dataStack和minStack为空

入栈：

• dataStack入栈
• minStack为空，minStack入栈
• minStack非空，且栈顶小于入栈元素，忽略
• minStack非空，且栈顶大于等于入栈元素，minStack入栈（当有多个相同min值入栈时，需要记录多次）

出栈：

• dataStack记录栈顶值top，并出栈
• top等于minStack栈顶值，minStack出栈

栈顶值：

• 返回dataStack栈顶值

最小值：

• minStack非空，返回minStack栈顶元素
• minStack为空，返回dataStack栈顶值

代码

type MinStack struct {
	dataStack []int
	minStack  []int
}

func Constructor() MinStack {
	return MinStack{
		dataStack: make([]int, 0),
		minStack:  make([]int, 0),
	}
}

func (this *MinStack) Push(x int) {
	this.dataStack = append(this.dataStack, x) // dataStack入栈
	if len(this.minStack) == 0 {               // minStack为空，minStack入栈
		this.minStack = append(this.minStack, x)
	} else {
		// minStack栈顶大于等于入栈元素，minStack入栈
		// 入栈 0 1 0时，minStack需要记录为[0,0]，否则当0出栈时min函数无法继续返回0
		if this.minStack[len(this.minStack)-1] >= x {
			this.minStack = append(this.minStack, x)
		}
	}
}

func (this *MinStack) Pop() {
	if len(this.dataStack) > 0 {
		top := this.dataStack[len(this.dataStack)-1]
		this.dataStack = this.dataStack[0 : len(this.dataStack)-1] // dataStack出栈
		if top == this.minStack[len(this.minStack)-1] {            // top等于minStack栈顶值，minStack出栈
			this.minStack = this.minStack[0 : len(this.minStack)-1]
		}
	}
}

func (this *MinStack) Top() int {
	if len(this.dataStack) > 0 {
		return this.dataStack[len(this.dataStack)-1]
	}
	return -1

}

func (this *MinStack) Min() int {
	if len(this.minStack) > 0 {
		return this.minStack[len(this.minStack)-1]
	} else if len(this.dataStack) > 0 {
		return this.dataStack[len(this.dataStack)-1]
	}
	return -1
}